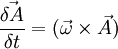Rotating frame transformation

From NMR Wiki

Revision as of 01:25, 20 March 2008 by Evgeny Fadeev (Talk | contribs)
Jump to: navigation, search

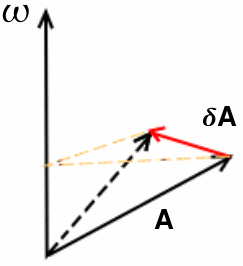
Let's start with a fixed laboratory frame. In that frame, imagine vector A rotating with a positive angular frequency ω. Direction of such rotation of A will be counter-clockwise.

image:rotation-vector.gif

Let's determine derivative 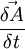\frac{\vec{\delta A}}{\delta t}.

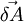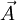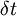First calculate \vec{\delta A} - how much \vec{A} changes within time \displaystyle \delta t.

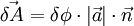
\vec{\delta A} = \delta\phi \cdot |\vec{a}| \cdot \vec{n}

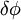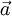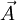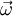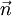In the equation above \displaystyle \delta \phi - rotation angle, \vec{a} - projection of \vec{A} on the plane normal to \displaystyle \vec{\omega}, and \vec{n} - unit vector collinear with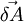 \vec{\delta A}

Notice that 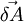\vec{\delta A} is normal to the plane formed by 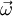\vec{\omega} and \vec{A}.

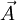Rotation angle can be expressed as

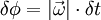
\delta \phi = |\vec{\omega}| \cdot \delta t

So, we have

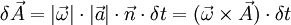
\delta \vec{A} = |\vec{\omega}| \cdot |\vec{a}| \cdot \vec{n} \cdot \delta t = (\vec{\omega}\times\vec{A}) \cdot \delta t

Therefore:

\frac{\vec{\delta A}}{\delta t} = (\vec{\omega}\times\vec{A})

Retrieved from "http://nmrwiki.org/wiki/index.php?title=Rotating_frame_transformation"
Personal tools
navigation
community
Contents
teaching
pulse sequences
experiments
software
reference