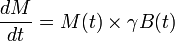Bloch equations
From NMR Wiki
Bloch equation describes evolution of classical magnetic moment in the magnetic field. The equation in the absence of T1 and T2 relaxation is:
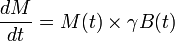
Summary explanation
A particle with a magnetic moment M in the magnetic field B will experience change of its mechanical angular moment J, i.e. torque = dJ/dt.
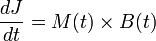
Wigner-Eckart theorem in quantum mechanics proves that particle's magnetic moment is collinear with it's angular moment so that:
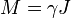 ,
,
where γ is the scalar quantity called gyromagnetic ratio of the particle.
Therefore we have expression (known as Bloch Equation):