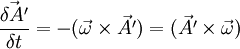Rotating frame transformation

From NMR Wiki

Revision as of 01:37, 20 March 2008 by Evgeny Fadeev (Talk | contribs)

(diff) ←Older revision | Current revision (diff) | Newer revision→ (diff)

Rotating vector in a fixed frame

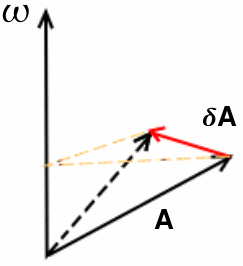
Let's start with a fixed laboratory frame. In that frame, imagine vector A rotating with a positive angular frequency ω. Direction of such rotation of A will be by convention - counter-clockwise.

Let's determine derivative 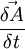$\frac{\vec{\delta A}}{\delta t}$ .

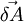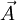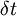First calculate $\vec{\delta A}$ - how much $\vec{A}$ changes within time $\displaystyle \delta t$ :

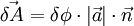
$\vec{\delta A} = \delta\phi \cdot |\vec{a}| \cdot \vec{n}$

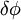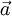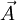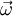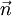In the equation above $\displaystyle \delta \phi$ - rotation angle, $\vec{a}$ - projection of $\vec{A}$ on the plane normal to $\displaystyle \vec{\omega}$ , and $\vec{n}$ - unit vector collinear with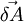 $\vec{\delta A}$

Notice that 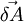$\vec{\delta A}$ is normal to the plane formed by 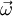$\vec{\omega}$ and $\vec{A}$ .

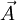Rotation angle can be expressed as

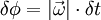
$\delta \phi = |\vec{\omega}| \cdot \delta t$

So, we have

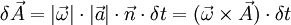
$\delta \vec{A} = |\vec{\omega}| \cdot |\vec{a}| \cdot \vec{n} \cdot \delta t = (\vec{\omega}\times\vec{A}) \cdot \delta t$

Therefore:

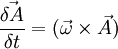
$\frac{\vec{\delta A}}{\delta t} = (\vec{\omega}\times\vec{A})$

Fixed vector in the rotating frame

If instead the vector is fixed in the laboratory frame, but the reference frame is rotating in the same direction and rate as above, our derivative within the rotating frame will simply equal above with the minus sign:

$\frac{\vec{\delta A'}}{\delta t} = -(\vec{\omega}\times\vec{A'}) = (\vec{A'}\times\vec{\omega})$

Retrieved from "http://nmrwiki.org/wiki/index.php?title=Rotating_frame_transformation"

Rotating frame transformation

From NMR Wiki

Rotating vector in a fixed frame

Fixed vector in the rotating frame

Views

Personal tools

navigation

community

Contents

Toolbox