Rotating frame transformation
From NMR Wiki
This tutorial needs review
Contents |
Introduction
Rotating frame transformation is often used in NMR spectroscopy to simplify description of magnetization vector in the magnetic field.
Perhaps it is easier to first calculate derivative of a vector rotating in a fixed laboratory frame and after that switch to the case of static vector and rotating frame.
In the end we can allow the vector change in the laboratory frame and get the final formula for derivative in the rotating frame.
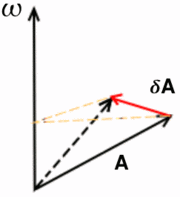
Rotating vector, fixed frame (1)
In fixed frame, imagine vector A rotating with a positive angular frequency ω. Direction of such rotation of A will be by convention - counter-clockwise.
Let's determine derivative 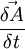 .
.
First calculate 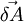 - how much
- how much 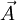 changes within time
changes within time 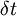 :
:
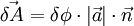
In the equation above 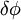 - amount of rotation that occurs during time
- amount of rotation that occurs during time 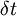 ,
, 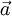 - projection of
- projection of 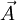 on the plane normal to
on the plane normal to 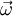 , and
, and 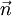 - unit vector collinear with
- unit vector collinear with 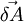
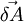 is essentially the length of the infinitesimal arc drawn by the tip of the vector
is essentially the length of the infinitesimal arc drawn by the tip of the vector 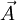 during the interval
during the interval 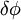
Rotating vector, fixed frame (2)
Notice that 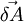 is normal to the plane formed by
is normal to the plane formed by 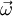 and
and 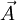 .
.
Rotation angle can be expressed as
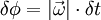
So, we have
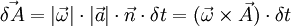
In the previous step the definition of vector cross product was used. Therefore:
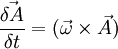
Fixed vector, rotating frame
If instead 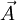 is fixed in the laboratory frame, but the reference frame is rotating in the same direction and rate as above, our derivative of vector within the rotating frame will simply equal above with the minus sign:
is fixed in the laboratory frame, but the reference frame is rotating in the same direction and rate as above, our derivative of vector within the rotating frame will simply equal above with the minus sign:
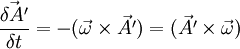
where 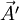 is coordinate of the vector in the rotating frame
is coordinate of the vector in the rotating frame
Full rotating frame transformation
Now we have 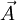 also changing in the static laboratory frame with a derivative
also changing in the static laboratory frame with a derivative 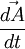 .
.
Then full transformation will look like:
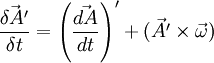
where 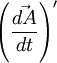 is
is 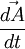 , recalculated in the new rotating coordinates.
, recalculated in the new rotating coordinates.