Analysis of HETLOC data

From NMR Wiki

(Redirected from Analysis of HETLOC data with Sparky)

HETLOC [1, 2] experiment can be used to obtain one, two, three and more -bond separated heteronuclear J couplings as well as their relative signs, which depend on the conformation and stereochemical arrangement of atoms in the molecule.

HETLOC experiment has a limitation that it won't show couplings to carbon atoms (or other X-nuclei to which HETLOC experiment might be tuned) not connected to a proton. That is because intrinsically HETLOC is a TOCSY experiment.

Before starting to analyze spectrum, list the couplings to be collected (chances are all observable couplings won't be needed).

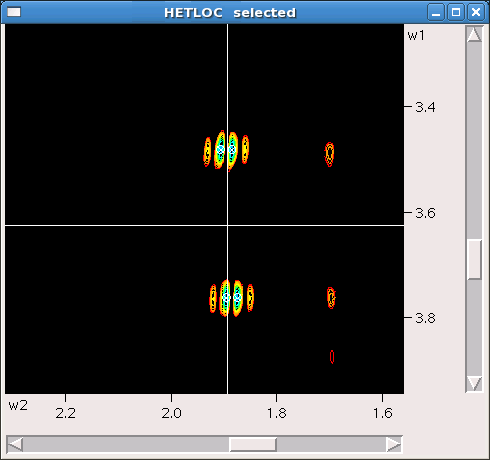
Then, open HETLOC spectrum, and for a given coupling between atoms C_x and H_y:

draw a horizontal line at ω1 (usually vertical dimension) = δ(H_x) - i.e. chemical shift of C_x-attached proton.
draw a vertical line at ω2 = δ(H_y)
alternatively move a cursor so that cross-hairs correspond to those lines
note the point of intersection of the two lines
somewhere symmetric to that point along the vertical line there might be two peaks or groups of peaks (i.e. if they are observable)
if the peaks appear to be missing - try redrawing spectrum at lower first contour level (~intensity scale in 2D plane)
two (groups of) peaks will be offset in ω1 by ¹JC_xH_x and in ω2 -by the sought value of ⁿJC_xH_y
take a careful note about sign of coupling - is the doublet tilted to the left or to the right (i.e. same as main dagonal?)