T1 measurement by inversion recovery
From NMR Wiki
Inversion Recovery
Here the spins are flipped to the 180° position, and sampled at different times until the spins are back in equilibrium. This will give a characteristic set of spectra, which can be used to accurately measure T1-Times for the sample. The delay τ is varied and the intensities in the spectra are plotted agains τ.
T1 fitting
Using a nonlinear regression algorithm, the data is fitted to the following model:
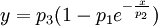
Which can be simplified (when using a normalised plot which has very little noise) to:
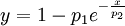
For an inversion recovery experiment 1 < p1 < 2 is normally true. In the optimal case, p1 would be 2, but since in reality one does not get a negative signal which is as strong as the maximum positive signal, the parameter p1 compensates for that. The parameter p2 is equal to T1.
When trying to fit multiple T1-Times in a samle, one simply fits a sum of several of the previous model. For two T1-Times, one would use:
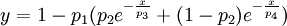
Here p1 is used as bevore, but p2 now serves as a parameter determining how much each of the two components contribute to the relaxation behaviour. The parameters p3 and p4 are the two contributing T1-Times.

